When working with very large or very small numbers in data science, computer will very often convert them to something that is easier to handle, easier to read, etc. So, the reasons behind scientific notation are practical and here we will see how to prevent it and how to handle it.
Examples
First, lets take a look what scientific notation looks like:
x <- 123456789101112131415
x
[1] 1.234568e+20
## This number 1.234568e+20 represents a scientific notation of number
## 123456789101112131415, which is stored in the data object x.
In this tutorial, you will learn how to disable scientific notation (e.g. 1.234568e+20) in the R programming language.
We can prevent this in multiple ways. Probably the most popular way it can be achieved is by disabling scientific notation in R (just exexute this line of code):
options(scipen = 999)
Now if you print out the x variable we defined earlier, you get exact value you defined:
> x
[1] 123456789101112131584
NOTE: By executing upper code, we changed general configuration for R settings. If you want to revert that, you can restart Rstudio.
If you want to have your default settings stored (to have them for the cases when you want to revert the changes of default configurations), you can store them in sepparate file:
default_options = options()
save(default_options, file = “default_options.rda”)
Now you can load those defaults from the file and apply them:
load(“default_options.rda”)
options(default_options)
So, the upper example is for preventing scientific notation for all numbers. Lets see how to prevent it for one specific number. To do this, we use format() function. The R format function enables us to prevent R from showing an exponential representation. Have a look at the following R code:
format(x, scientific = FALSE) # Apply format function in R
[1] “123456789101112131584”
As you can see, the whole number with all digits was returned to the RStudio console.
Lets quickly remind ourselves how to convert characters to numeric:
as.numeric(“123456789101112131584”)
[1] 123456789101112131584
Theory and explanations
Scientific notation is a way of expressing numbers that are too big or too small to be conveniently written in the layman’s way, the decimal form. What happens is that the number gets expressed in ‘times ten raised to the power of…’. Here are some examples from Wikipedia:
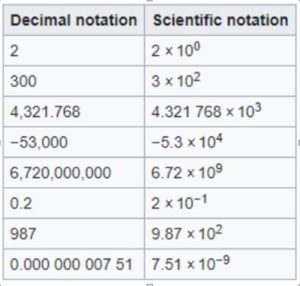
In R, we use the E-notation. For example, one billion will be expressed as 1e+09. In your head, you can simply replace the e with 10 and anything after that is the power to which you raise it.
This is important because in science we often deal with numbers that are either very small or very big.
For example, this is distance between Earth and the closest star outside of a solar system:
25,300,000,000,000 miles.
Other extreme is very small number, for example the average speed of light to travel 5 meters:
0.000 000 0203 seconds.
If we were to talk about the atomic particles, we would talk about numbers so large and so low that even with usage of calculator or computer would be complicated!
Scientific notations is the more compact way to use these numbers.
Here I will show you how to convert number to scientific notation:
Lets take this number „25,300,000,000,000 miles.“
regularExpression <- 2,5 300 000 000 000,
New decimal places are on the end of a number and on the spot where we only have on number to the left, which is after first number.
Here I count the digits between the commas, which is 13.
Now I write the number with the decimal place in the new position and I get rid of the all zeros after number 3. So the new number is going to be 2.53 and that is first part.
In my regularExpression variable, I have 13 numbers between two commas and we acknowledge that by rising 10 to the power of 13, so its going to be :
2.53 x 1013
I moved the decimal place for 13 places and that is why it is to the power of 13.
Now lets see how to do this with small numbers. Its same as with big numbers, but with difference of exponent on number 10 getting smaller.
For example:
regularExpression <- 0,000 000 02,03
I have commas after first digit (which is 0) and after the first digit which is not 0 and that is 2.
Between the commas, I have 8 digits. Now we rewrite our number with decimal place in its new position, which is 2,03
In my regularExpression variable, I have 8 numbers between two commas and we acknowledge that by rising 10 to the power of -8, so it’s going to be :
2.03 x 10-8
Let’s take a look at another example of scientific notation on big numbers.
X <- 3,749 000 000 ,
In this number, decimal place is moved for 9 spots so its going to be x 109
Before first zero, we have 3,749 and that means that scientific notation for number X is:
3,749 x 109
Lets see yet another example for small numbers.
Y<- 0.00004269
First number that is not zero is 4. That means that our new decimal place is after 4, so it will be like this:
Y<- 000004.269
We moved decimal place for 5 digits. That means that will be x 10-5
From
the number Y, we erase zeroes and we are left with 4.269
So, the scientific notation of Y number will be 4,269 x 10-5
Lets see now how to convert scientific notations to real numbers. For example:
7.921 x 108
To get real number from this, I must have 8 digits after decimal place. I already have 3 of them (921),
and for the rest I add zeros. That means I will have 7.92100000
In the end, I simply remove comma (decimal place) and I get real number which is 792100000.
Let’s see how to do this for small numbers. For example:
8.2 x 10-5
Here
we move decimal place to the left. 10-5 means that we must have 5 digits before current decimal place
(8.2)
That means that we add zeroes before 8 till we have five digits before number
2:
00008.2
After this, we move decimal place to the very left:
.000082
And this is our number
To learn more about scientific notation, check out this tutorial: